GOSUB. So I used the Versatile Commodore Emulator (VICE) instead.The First Test.
1000 CLR 1010 PRINT "test one "; 1020 i=1 1030 GOSUB 9000 1040 IF pf(0)<>0 THEN PRINT "expected no factors" : STOP 1050 PRINT "green"Number
i is the value to be factored and the array pf is expected to contain the number of prime factors in pf(0) followed by the factors themselves on return of the "generate" function (line 9000).test one ?UNDEF'D STATEMENT ERROR IN 1030Add the function.
8990 END 9000 REM ----- function generate 9010 REM in ... i ... number 9020 REM out ... pf() ... factors 9030 RETURNRun the test.
test one greenThe Second Test.
1100 CLR 1110 PRINT "test two "; 1120 i=2 1130 GOSUB 9000 1140 IF pf(0)<>1 THEN PRINT "expected 1 factors:";pf(0) : STOP 1150 IF pf(1)<>2 THEN PRINT "expected factor 2:";pf(1) : STOP 1160 PRINT "green"
test one green test two expected 1 factors: 0 BREAK IN 1140
9000 REM ----- function generate 9030 IF i=1 THEN RETURN 9040 pf(0)=1 9050 pf(1)=2 9060 RETURNUnfortunately there is no such thing as "BUnit". So I have to create testing infrastructure along the way. Keeping the tests green helps during the extraction of an "assert" method (line 100).
80 GOTO 1000 90 REM ***** test infrastructure ***** 100 REM ----- method assert equals(int) 110 REM in ... me$ ... message 120 REM in ... ex ... expected 130 REM in ... ac ... actual 140 IF ex=ac THEN RETURN 150 PRINT "red" 160 PRINT me$;" expected";ex;" but was";ac 170 STOP 180 RETURN ... 1100 CLR 1110 PRINT "test two "; 1120 i=2 1130 GOSUB 9000 1140 ex=1 : ac=pf(0) : me$="num factors" : GOSUB 100 1150 ex=2 : ac=pf(1) : me$="1st factor" : GOSUB 100 1160 PRINT "green"The Third Test.
1220 i=3 1230 GOSUB 9000 1240 ex=1 : ac=pf(0) : me$="num factors" : GOSUB 100 1250 ex=3 : ac=pf(1) : me$="1st factor" : GOSUB 100Run the test.
test one green test two green test three red 1st factor expected 3 but was 2 BREAK IN 170Modify the function.
9050 pf(1)=iGreen again. After the third test it's getting boring. The tests should be refactored to be more DRY:
200 REM ----- method teardown 210 PRINT "green" 220 RETURN 300 REM ----- method setup 310 REM in ... me$ ... test name 320 PRINT "test ";me$;" "; 330 RETURN 400 REM ----- method assert prime factors 410 READ me$ 420 GOSUB 300 430 READ i 440 GOSUB 9000 450 READ af 460 ex=af : ac=pf(0) : me$="num factors" : GOSUB 100 470 IF af=0 THEN GOTO 520 480 FOR j=1 TO af 490 READ ex 500 ac=pf(j) : me$=STR$(j)+". factor" : GOSUB 100 510 NEXT 520 GOSUB 200 530 RETURN 990 REM ***** test cases ***** 1000 DATA "one", 1, 0 1010 GOSUB 400 1100 DATA "two", 2, 1, 2 1110 GOSUB 400 1200 DATA "three", 3, 1, 3 1210 GOSUB 400The Fourth Test.
1300 DATA "four", 4, 2, 2, 2 1310 GOSUB 400
9000 REM ----- function generate 9010 REM in ... i ... number 9020 REM out ... pf() ... factors 9025 REM local ... nf ... number factors 9030 nf=0 9040 pf(0)=nf 9050 IF i=1 THEN RETURN 9060 IF INT(i/2)*2=i THEN nf=nf+1 : pf(nf)=2 : i=i/2 : GOTO 9040 9070 nf=nf+1 : pf(nf)=i : i=1 : GOTO 9040 9080 RETURNLine 9070 is more than needed to get the fourth test green, but it's the first thing that came to my mind.
The Fifth Test.
1400 DATA "five", 6, 2, 2, 3Works as well, no changes needed.
The Sixth Test.
1500 DATA "six", 8, 3, 2, 2, 2Again this still works, I "cheated" a bit.
The Seventh Test.
1600 DATA "seven", 9, 2, 3, 3Now I really need the nested loops.
9000 REM ----- function generate 9010 REM in ... i ... number 9020 REM out ... pf() ... factors 9030 REM mod ... ca ... pf candidate 9040 pf(0)=0 : REM special case 9050 IF i=1 THEN RETURN 9060 IF INT(i/2)*2<>i THEN GOTO 9110 9070 pf(0)=pf(0)+1 9080 pf(pf(0))=2 9090 i=i/2 9100 GOTO 9050 9110 FOR ca=3 TO INT(SQR(i)) STEP 2 9120 IF i=1 THEN RETURN 9130 IF INT(i/ca)*ca<>i THEN GOTO 9180 9140 pf(0)=pf(0)+1 9150 pf(pf(0))=ca 9160 i=i/ca 9170 GOTO 9120 9180 NEXT 9190 RETURNThis includes already two performance optimisations: Handling the special case 2 up front to be able to use
STEP 2 and skip every second prime factor candidate. Second using the square root of i as upper bound for the loop. But there is a bug not covered by the tests. Can you spot it? Yet another refactoring to remove duplicate code of adding prime factors to pf.9040 pf(0)=0 : ca=2 : REM special case 9050 IF i=1 THEN RETURN 9060 IF INT(i/ca)*ca=i THEN GOSUB 9200 : GOTO 9050 9070 FOR ca=3 TO INT(SQR(i)) STEP 2 9080 IF i=1 THEN RETURN 9090 IF INT(i/ca)*ca=i THEN GOSUB 9200 : GOTO 9080 9100 NEXT 9110 RETURN 9200 pf(0)=pf(0)+1 9210 pf(pf(0))=ca 9220 i=i/ca 9230 RETURNI could still get rid of the duplicate lines 9060 and 9090...
Another Test.
1700 DATA "eight", 10, 2, 2, 5This reveals the bug in line 9070. If the value contains different prime factors then the last factor is lost. We need another check in line 9110.
9100 NEXT 9110 IF i>1 THEN ca=i : GOSUB 9200 9120 RETURNEND.
One last refactoring to add colours and time measurements to methods "setup" (line 300) and "teardown" (line 200). Two more tests to see the performance of larger (32719) values of
i. The function even works for 2^31-1 (huge), but takes quite some time, although the loop is already optimised.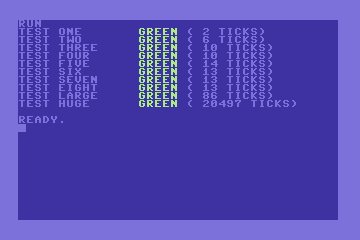 (Download the source.)
(Download the source.)







1 comment:
[...] performed the kata in all programming languages which I know, e.g. Java, Ruby and even old BASIC or Turbo Pascal and recently using XSL transformations. [...]
Post a Comment